Przeprowadzona analiza statystyczna nie pozwala stwierdzić, że przebieg epidemii koronawirusa w Polsce został sfałszowany jako całość. Istnieją jednak poszlaki sugerujące możliwość manipulacji w wybranych tygodniach.
- Przeprowadzona przeze mnie analiza danych dotycących zakażeń, zgonów i wyzdrowień i porównanie ich z rozkładem Benforda wskazuje na naturalne pochodzenie opisujących je liczb. Podobne analizy wykonano wcześniej dla kilkunastu krajów i stwierdzono duże prawdopodobieństwo fałszowania danych w Rosji i podejrzenie manipulacji w Iranie.
- Analiza odchyleń w raportowanych wynikach, którą przeprowadził naukowiec z Torunia, Profesor Boudewijn François Roukema, sugeruje możliwość manipulacji danymi w tygodniu poprzedzającym pierwszą turę wyborów prezydenckich w Polsce w czerwcu 2020.
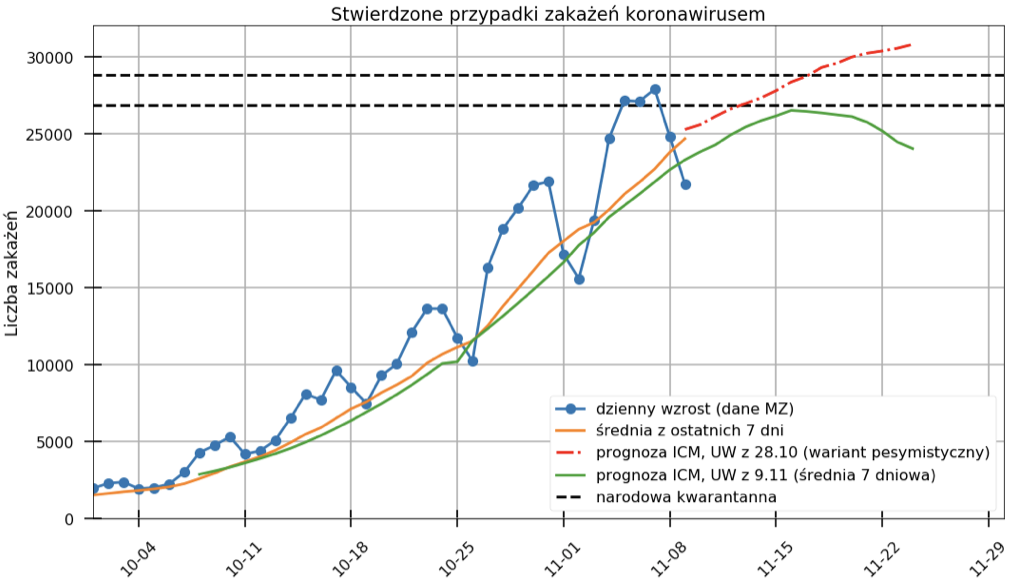
- Wskazane przez Michała Rogalskiego rozbieżności w danych podawanych przez Ministerstwo Zdrowia i stacje sanepidu, pokazują że gdyby uwzględnić „zgubione” dane, to 11 listopada 2020 przekroczyliśmy próg „narodowej kwarantanny”.
- Nawet jeśli przyjąć, że dostępne dane nie są efektem celowo prowadzonej „kreatywnej księgowości” to codzienne raporty odnośnie nowych zakażeń nie oddają dobrze obrazu rozwoju epidemii. Codzienne wyniki podlegają dużym wahaniom, a osoby podejrzewające zakażenie coraz mniej chętnie poddają się testom.
Rozkład Benforda
Jednym ze sposobów sprawdzenia wiarygodności dostępnych danych jest porównanie ich z modelami matematycznymi, zgodnie z którymi powinno zachowywać się dane zjawisko. W przypadku liczby zakażeń koronawirusem zauważono, że obserwowane liczby zakażeń spełniają rozkład Benforda.
Rozkład Benforda to reguła matematyczna, która opisuje częstość występowania określonej pierwszej cyfry w rzeczywistych danych statystycznych. Zgodnie z rozkładem Benforda najczęściej w zbiorach danych (takich jak np. powierzchnie jezior, dane z roczników statystycznych, wartości stałych fizycznych) obserwujemy liczby, które zaczynają się cyfrą 1. W ogólności im wyższa cyfra tym rzadziej pojawia się na pierwszym miejscu w naturalnie występujących liczbach.
| Pierwsza cyfra | Częstość |
|---|---|
| 1 | 30,1% |
| 2 | 17,6% |
| 3 | 12,5% |
| 4 | 9,7% |
| 5 | 7,9% |
| 6 | 6,7% |
| 7 | 5,8% |
| 8 | 5,1% |
| 9 | 4,6% |
Jeśli słyszycie o tym prawie po raz pierwszy to prawdopodobnie wydaje się Wam nielogiczne. Bo dlaczego akurat liczby z niskimi początkowymi cyframi miały by być uprzywilejowane i częściej występować w naturze? Też się nad tym zastanawiam i szczerze mówiąc, nie wiem czy istnieje zadowalające wyjaśnienie tego faktu inne niż to, że zaobserwowano taką zależność i była ona na tyle intrygująca, że ktoś ją opisał i nazwał. Rozkład Benforda najlepiej sprawdza się w przypadku wielkości, które przyjmują wartości w zakresie co najmniej kilku rzędów wielkości. Dla przykładu, rozkład ten nie będzie spełniony w analizie liczby mieszkańców w miejscowościach mających od 100 do 900 mieszkańców, ale będzie się uwidaczniał w danych dotyczących miejscowości mających od 10 do 10 000 mieszkańców. Rozkład Benforda jest tak powszechny, że jest stosowany m.in. do sprawdzania poprawności zeznań podatkowych czy wykrywania defraudacji, gdyż ludzie wpisując liczby tak, żeby wydawały się przypadkowe, nie są świadomi, że pewne cyfry powinny występować częściej na pierwszej pozycji.
Więcej o rozkładzie Benforda możecie przeczytać m.in. w artykule z czasopisma Delta.
Rozkład Benforda a dane dla Polski
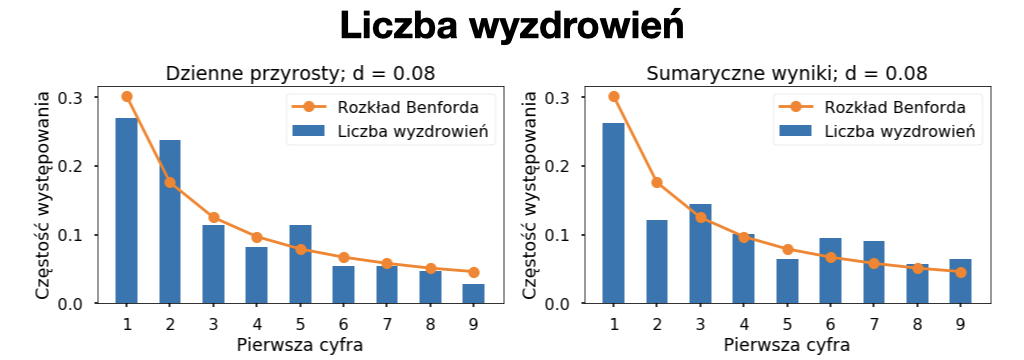
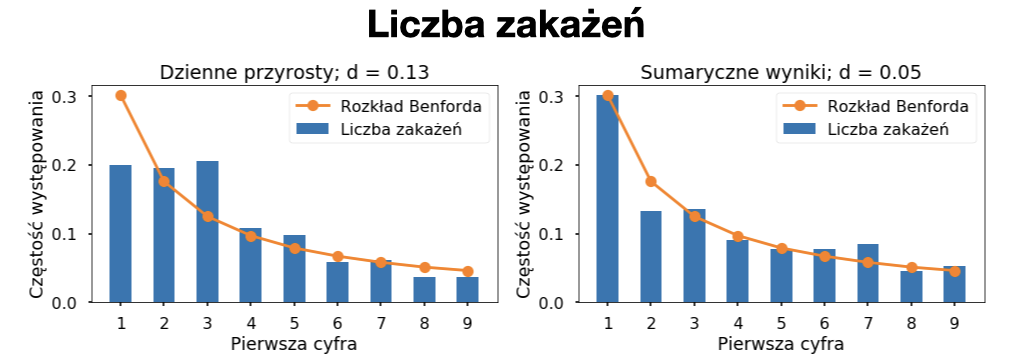
Poprzednia analiza danych dotyczących koronawirusa z wykorzystaniem rozkładu Benforda, wskazała na duże prawdopodobieństwo fałszowania danych w Rosji i podejrzenie manipulacji w Iranie. Niestety badanie to nie uwzględniało danych z Polski. Dlatego wykonałem podobną analizę dla danych z naszego kraju, od początku epidemii w polsce do 4 stycznia 2021. Na wykresach poniżej możecie zobaczyć porównania rzeczywistych danych z idealnym rozkładem Benforda. Żeby określić podobieństwo obserwowanego rozkładu do rozkładu Benforda wprowadzony został parametr „d”, który przyjmuje wartości od 0 do 1. Parametr „d” jest równy 0 gdy rzeczywiste dane idelanie pokrywają się z rozkładem teoretycznym, natomiast „d” = 1 gdy rzeczywiste dane są najbardziej odległe od tego rozkładu (gdyby wszystkie liczby zaczynały się od cyfry 0). Wartości parametru „d” bardzo rzadko są bliskie 0 dla rzeczywistych zbiorów danych i dopiero wartości powyżej 0,25 wskazują na możliwość występowania nieprawidłowości czy manipulacji danymi.
Powyższe wykresy po lewej stronie przedstawiają analizę codziennie raportowanych liczb (nowych zakażeń, zgonów i wyzdrowień), a po prawej ich codziennych sumarycznych wartości. Już na pierwszy rzut oka widać, że we wszystkich zbiorach liczby z niższymi początkowymi cyframi pojawiają się częściej niż z wyższymi. Dla żadnego z analizowanych przypadków odległość od idealnego rozkładu Benforda nie jest większa niż 0,25. Największe odchylenie d = 0,18 obserwujemy dla sumarycznej liczby zgonów, jednak podobnego odchylenia nie widać w dziennych liczbach. Obserwowane liczy zgonów (na szczęście) są zdecydowanie niższe niż liczby zakażeń i wyzdrowień, obejmują najmniejszy zakres wartości, w związku z czym nie jest zaskoczeniem, że mogą charakteryzować się najwyższym odchyleniem od idealnego rozkładu. Drugim najwyższym odchyleniem „d” = 0,13 charakteryzują się dzienne liczby zakażeń. Nie jest to odchylenie, które powinno być alarmujące. Uwagę niektórych na pewno jednak zwróci znaczna „wizualna różnica” między rozkładem teoretycznym i rzeczywistym. Musimy jednak pamiętać, że przez około pół roku mieliśmy do czynienia z tzw. „pełzającą epidemią” i dzienne liczby zakażeń zawierały się w przedziale ok 200 – 800 (czyli nie przekraczały więcej niż jednego rzędu wielkości) zatem takie odchylenie jest jak najbardzie w normie. Dla porównania jak wyglądają dane, co do których istnieje podejrzenie fałszerstwa załączam analizę dziennych zakażeń z Rosji [źródło].

Podsumowując: Gdyby dane dotyczące rozwoju pandemii w Polsce były przez cały czas fałszowane, to byłoby to bardzo dobre fałszerstwo. W momencie gdy dostępne były liczby z poszczególnych stacji sanepidu było praktycznie niemożliwe, żeby ktoś wymyślał wszystkie wartości w taki sposób, aby ich sumy układały się w poprawny rozkład Benforda. Nie oznacza to jednak, że można mieć 100% pewność iż do manipulacji w ogóle nie dochodziło.
Analiza odchyleń
W lipcu 2020 Profesor Roukema opublikował w serwisie arxiv.org artykuł, w którym przeanalizował dane epidemiczne z 68 krajów i skupił się na występujących w nich odchyleniach (wahaniach pomiędzy wynikami z poszczególnych dni). W znaczącej większości krajów rozkład opisujący odchylenia w wynikach cechował się zmiennością większą niż rozkład Poissona. Właściwość taką po angielsku opisuje się jako „super-Poissonian” i według autora jest ona charakterystyczna dla danych epidemicznych, gdy wahania biorą się zarówno z samej natury rozprzestrzeniania się epidemii jak i administracyjnych procesów związanych z testowaniem czy raportowaniem wyników. Wśród krajów, z których dane epidemiczne cechowały się zaskakująca małymi odchyleniami znalazły się m. in.: Indie, Rosja, Algieria i Białoruś. Uwagę autora zwróciła także bardzo specyficze właściwości danych dla Polski w okresie 7 dni przed pierwszą turą wyborów prezydenckich 28 czerwca 2020. Analiza wykazały, że w tym okresie dane cechowały się wyjątkowo niskim poziomem wahań, według autora co najmniej 10-krotnie mniejszym niż wcześniej. Co więcej autor zwraca uwagę na widoczny w tym okresie spadek wyników poniżej istotnej wówczas psychologicznej granicy 300 przypadków dziennie.
Podsumowując: Obserwacje te nie pozwalają jednoznacznie stwierdzić czy dane rzeczywiście były manipulowane czy nie. Dają jednak powód do zastanowienia się nad wpływem polityki informacyjnej rządu w sprawie koronawirusa na decyzje i zachowanie obywateli.
Kreatywna księgowość
Opisane powyżej analizy wymagają naukowego podejścia, niezłej znajomości statystyki, matematyki czy programowania i poświęcenia czasu na przeprowadzenie wnikliwych analiz. Ale nieścisłości w danych można dostrzec też gołym okiem bez zawiłych wzorów i skomplikowanych analiz. Jako pierwszy uwagę na nieścisłości w liczbach zakażeń w regionach i w całym kraju zwrócił Michał Rogalski, który od początku epidemii w Polsce prowadzi ogólnodostępną bazę danych epidemicznych. 12 listopada informował on, że różnica w danych wynosiła już 11 tysięcy zakażeń. Gdy Ministerstwo Zdrowia wzięło się za sprawdzenie sprawy okazało się, że liczba „zagubionych” przypadków przekroczyła 22 tysiące zakażeń. Co ciekawe, wszystko to działo się w bardzo ciekawym momencie, akurat wtedy gdy cała Polska wstrzymywała oddech w oczekiwaniu na to, czy przekroczymy próg wprowadzenia „kwarantanny narodowej”, czy nie. Późniejsze analizy Michała Rogalskiego wskazały, że kwarantanna powinna zostać wprowadzona 11 listopada. Sytuację obrazują dwa poniższe wykresy. Zagubione dane dorzucono bez podziału na konkretne daty i zaraportowano 24 listopada. Nie miało to już wpływu na decyzję odnośnie wprowadzenia kwarantanny w całym kraju.
Podsumowując: Nie ma dowodów na celową manipulację, ale ciężko pogodzić się z tak ciekawym zbiegiem okoliczności, że zagubienie danych nastąpiło akurat gdy byliśmy na kursie na pełny lock-down.
Rzeczywisty obraz epidemii
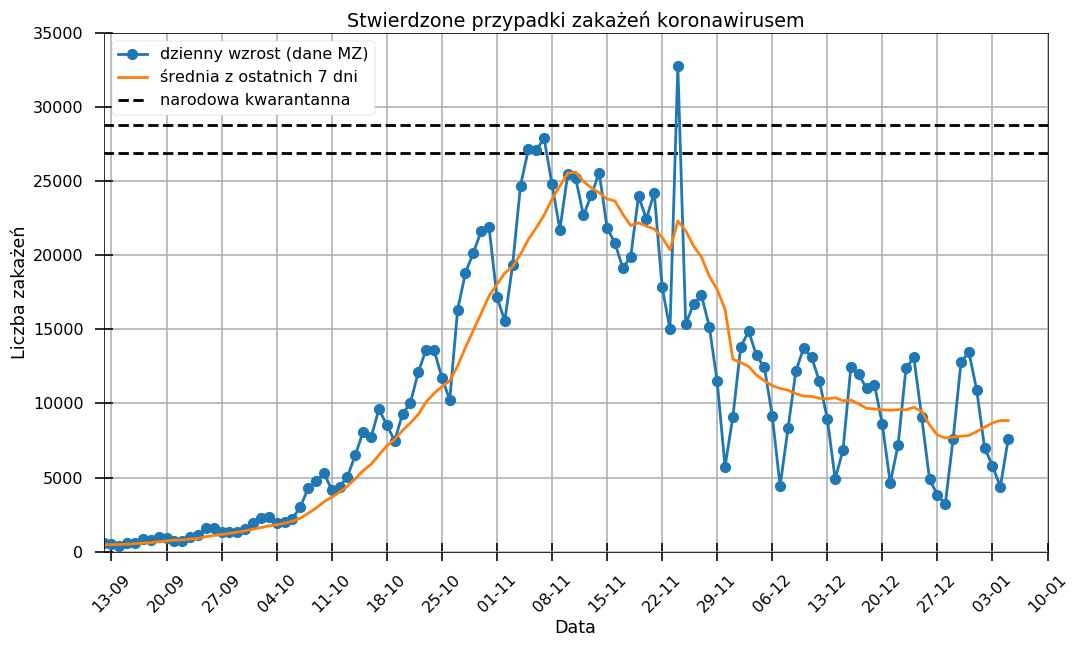
Załóżmy jednak, że danymi nikt nie manipuluje i wykryte zaburzenia w danych nie wynikały ze złej woli. Czy analizując codzienne raporty o zakażeniach możemy poznać prawdziwą sytuację w kraju? W momencie gdy nawet Ministerstwo Zdrowia zaczęło brać pod uwagę 7-dniową średnią liczbę zakażeń jako parametr do oceny sytuacji pomyślałem, że wszyscy już zauważyli jakim wahaniom podlegają dzienne raporty. Po każdym weekendzie czy wolnym dniu obserwujemy tzw. „efekt poniedziałku” gdy wyniki są zaniżone i w kolejnych dniach odbijają. Nadal jednak nie zauważyły tego serwisy informacyjne, które każde najmniejsze wahanie potrafią okrasić krzykliwym komentarzem mówiącym, że „znów dużo gorzej”, albo „sytuacja coraz lepsza”. Jak widać na wykresie poniżej, średnia tygodniowa licba zakażeń w ciągu ostatnich 30 dni była zdecydowanie niższa niż w listopadzie 2020.
Czy to znaczy, że sytuacja rzeczywiście się poprawiła? Tego niestety nikt nie wie. Lekarze już od jakiegoś czasu informują o tym, że liczba chętnych na testy się zmniejsza (artykuł z 25 listopada), a do szpitali zgłaszają się pacjenci w wyjątkowo ciężkim stanie. Sytuację tę skomentował też niedawno premier, mówiąc:
„Mniej ludzi chce się testować. My zachęcamy do testowania. Testy w ostatnich dniach to 25-30 tysięcy. Infrastruktura jest przygotowana na niewiele mniej niż 100 tysięcy dziennie. Niestety wiemy, że osoby, które spędzały święta, sylwestra w mniejszych liczbach chcą się testować. Dzisiaj być może nie wyłapujemy wszystkich zakażonych i sądzę, że te 5 tysięcy osób nie jest liczbą, która w pełni oddaje obraz dzisiejszej epidemii”
To ciekawa zmiana taktyki u premiera. Około miesiąc temu, w poniedziałek 30 listopada, czyli gdy obserowaliśmy typowy poniedziałkowy spadek zakażeń, a lekarze od co najmniej kilku dni mówili o spadku zainteresowań testami, premier pisał:
Dane nie kłamią. Proszę spojrzeć na wykres. Wygrywamy z epidemią! Liczba zakażeń spada!
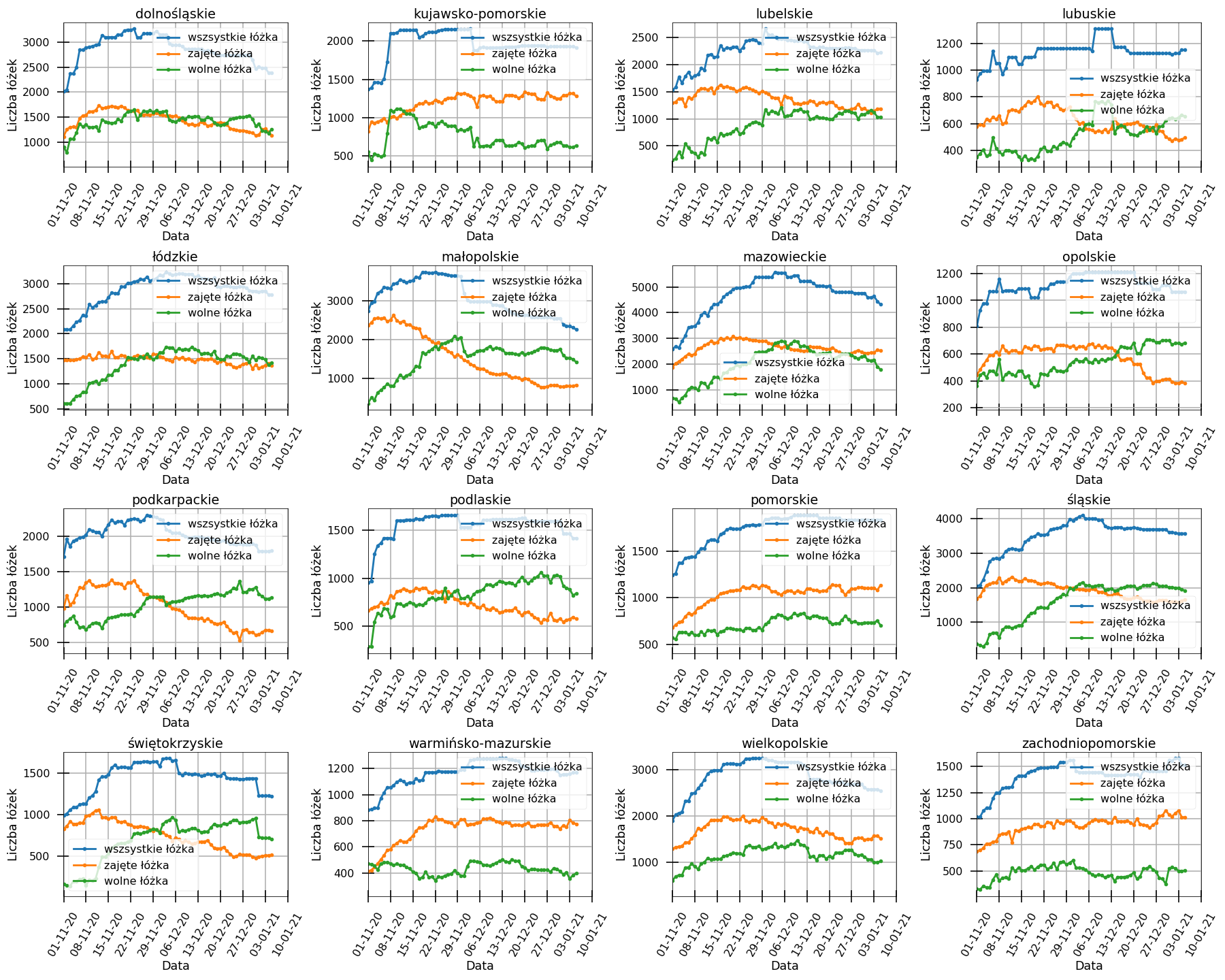
Zatem w jaki sposób można określić jak aktualnie rozwija się sytuacja epidemiczna w naszym kraju? Jednym z parametrów, który nie jest całkowicie zależny od liczby przeprowadzanych dziennie testów, jest liczba łóżek w szpitalach, które zajęte są przez pacjentów z koronawirusem. Jak widać, na pomarańczowych krzywych na wykresach poniżej, w większości województw krzywwe te nie odzwierciedlają spadków obserwowanych w dziennych liczbach zakażeń.
Podsumowując: Premier ma rację, mówiąc że nie jest tak dobrze jak wynikałoby ze spadku obserowanych dziennych liczb zakażeń. Ciężko jednak powiedzieć, jak zła jest aktualnie sytuacja. Dlatego ważne jest abyśmy wszyscy mogli się jak najszybciej zaszczepić!
Dodatkowa lektura:
- O rozkładzie Benforda po polsku: http://www.deltami.edu.pl/temat/matematyka/zastosowania/2016/03/21/Pierwsze_cyfry/
- Rozkład Benforda w analizie danych koronawirusa: https://www.researchgate.net/publication/344164702_Is_COVID-19_data_reliable_A_statistical_analysis_with_Benford’s_Law
- Odległość między danymi, a rozkładem Benforda: https://rss.onlinelibrary.wiley.com/doi/full/10.1111/j.1740-9713.2016.00919.x
- Artykuł profesora Roukemy: https://arxiv.org/pdf/2007.11779.pdf
- Wywiad z Michałem Rogalskim: https://www.polsatnews.pl/wiadomosc/2020-11-23/koronawirus-w-polsce-w-rzeczywistosci-przekroczylismy-prog-narodowej-kwarantanny/